# Binary Search
Binary Search is a searching algorithm which is used to quickly find a value in a sorted sequence of elements.
It uses divide and conquer strategy to find the element.
It is an efficient search algorithm as compared to linear search.
Elements must be sorted in order to use Binary Search.
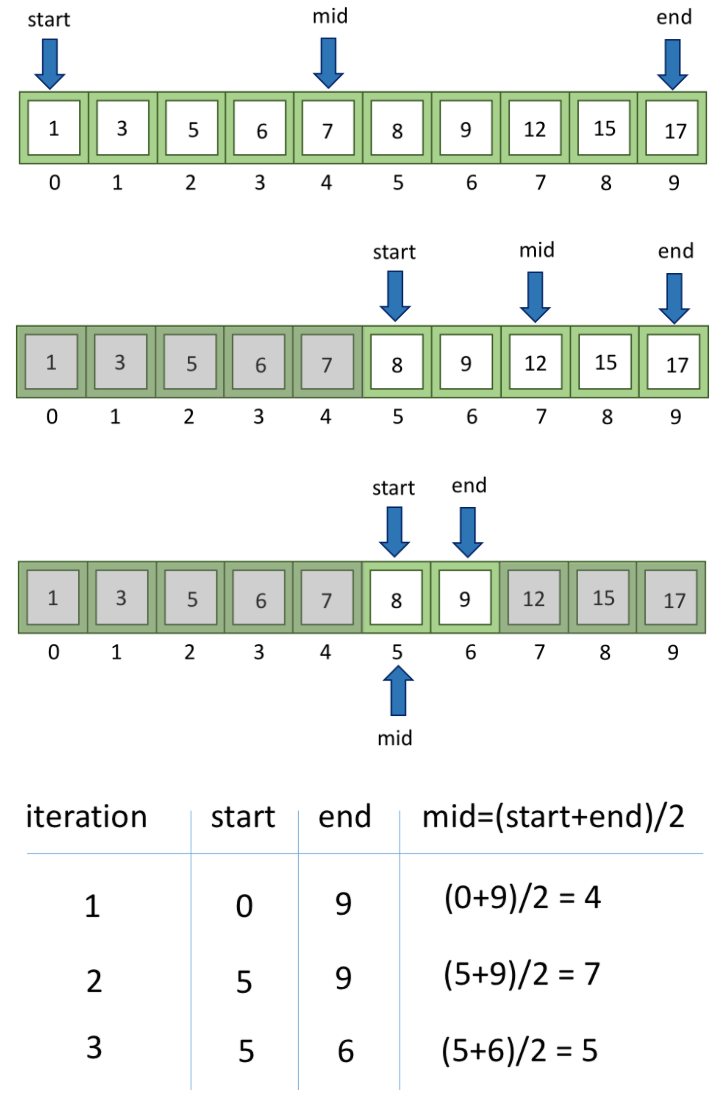
We will divide the search space (array) in two parts using variables:
start- initially 0.midend- initially n-1 where n is number of elements of the array
Calculate
mid = (start + end)/2Check if the element at mid is equal to the element we are looking for, if yes then element found.
If not, then check if element we are looking for is greater than (>) or less than (<) the element at mid.
- If greater:
start = mid+1 - If less:
end = mid - 1
- If greater:
Repeat steps 6,7,8 untill we find the element or start becomes greater than end which is the exit condition i.e. we will loop untill
start <= endSuppose in the example we are looking for element 8.
Element 8 found at index 5.
# Source Code - C++
#include <iostream>
using namespace std;
//Function to perform Binary Search
int BinarySearch (int A[], int n, int e)
{
int start, end, mid;
start = 0;
end = n-1;
while( start <= end )
{
mid = (start + end)/2;
if( A[mid] == e)
return mid;
else
if( e > A[mid])
start=mid+1;
else if( e < A[mid])
end = mid-1;
}
return -1;
}
//Main Function
int main() {
int n;
cout<<"enter size of array\n";
cin>>n;
int A[n],e,i,ans;
cout<<"enter elements of array\n";
for(i=0;i<n;i++)
cin>>A[i];
cout<<"enter element to be found\n";
cin>>e;
ans=BinarySearch(A,n,e);
if(ans==-1)
cout<<"not found\n";
else
cout<<"Found at index:"<<ans;
return 0;
}
Time Complexity: O(log n)



